Incremental Functional Aggregate Queries

This blog post concludes a research project I've done together with Frank McSherry ^[1] earlier this year at ETH Zurich.
In 2015 Khamis, Ngo and Rudra presented their paper, somewhat confusingly named, FAQ: Questions asked frequently ^[2] (that by the way makes it quite hard to google it).
It introduces a general framework to solve a variety of computational problems following ideas from database and relational algebra research.
That framework is called Functional Aggregate Query.
I implemented a simple version of it using the excellent differential dataflow ^[3] library in the Rust programming language.

This blog post is structured in the following way:

• An intuitive motivation and explanation of FAQ

• A bit of formalism

• Differential dataflow and how we can use its internals to implement FAQ

• How we then go on and incrementalize FAQ's

Introduction

What's this paper about?

Its major contribution is the insight that there is a common algebraic structure that seemingly unrelated problems share and that there is a general framework to efficiently solve these.

So what do problems like matrix chain multiplication, triangle counting or constrain satisfaction share? They are all special instances of what the authors refer to as a Functional Aggregate Query (FAQ) problem.

Let's have a look at two of them:

Matrix Chain Multiplication

Given a series of matrices $\boldsymbol{A}_{1},...,\boldsymbol{A}_{n}$ what is the product of these? We can reformulate this problem by identifying the matrices $\boldsymbol{A}_{n}$ as functions of two variables:

$$\psi_{i. i+1}: \text{Dom}(X_{i}) \, \times \, \text{Dom}(X_{i+1}) \rightarrow \mathcal{F}$$

where $\psi_{i, i+1}(x,y) = (\boldsymbol{A}_{i})_{xy}$ and $\mathcal{F}$ is a Field The problem then is to compute:

$$\phi (x_1, x_{n+1}) = \sum_{x_2 \in \text{Dom}(X_2)} ... \sum_{x_{n} \in \text{Dom}(X_{n})} \prod_{i=1}^{n}\psi_{i, i+1}(x_{i}, x_{i+1})$$

Triangle Counting

We want to compute the number of triangles in a given graph $G = (V, E)$. If we choose to represent edges in the graph $G$ in the following way:

$$\psi(u,v) = \begin{cases} 1 & \text{if} \, \{u,v\} \in E, u < v \\ 0 & \text{otherwise}. \end{cases}$$

The problem then becomes to compute:

$$\phi = \sum_{x_{1} \in V} \sum_{x_{2} \in V} \sum_{x_{3} \in V} \psi(x_{1}, x_{2}) \cdot \psi(x_{1}, x_{3}) \cdot \psi(x_{2}, x_{3})$$

Generally speaking these functions $\psi_{S} : \prod_{i \in S} \text{Dom}(X_{i}) \rightarrow \boldsymbol{D}$ also referred to as factors, map specific values of their input variables to some domain. For our purpose, we can think of these functions as relations over their variables. But instead of their Domain $\boldsymbol{D}$ simply being an identifier if there exists an instance of this specific relation we may choose a different one. Like the real numbers, sets, and so on.
We represent the values our factors take as a table, also called listing representation. We list all non-zero instances of our relation, $\psi_{S}$:

$$\langle \boldsymbol{x}_{S}, \psi_{S}(\boldsymbol{x}_{S})\rangle$$

Whereas $\boldsymbol{x}_{S}$ represent the support of the variable $\boldsymbol{x}$. In other words a specific tuple of variables and the corresponding value of the factor. The listing representation of a matrix factor for example looks like that:

$$\begin{gathered} \langle (1, 1), 1\rangle \langle (1, 2), 2\rangle \\ \langle (2, 1), 3\rangle \langle (2, 2), 4\rangle \end{gathered}$$ $$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$

The listing representation of our triangle example is simply a table of all edges in our graph, with their value being 1.

The solution to those examples follows the following formula:

1. Choose a variable order

2. Collect the set of factors that intersect with the first variable in our order

3. Multiply all values from the listing representation

4. Eliminate the given variable with the provided monoid operation

5. Push the resulting new factor into the next iteration

How can we represent these steps? First a few thoughts about the monoid operations that are part of the semiring.

If we identify factors as relations, multiplication might be naturally expressed as a join operation. We can join two relations along one of their attributes and produce a new one. In the relational algebra land, a tuple of a given relation only has two possible states. It exists or it does not. If we go on and extend this to allow values to be other then a boolean identifier, say the rational numbers, we can represent the multiplication monoid in the FAQ setting via a join operation.

Aggregations appear to be a fold or reduce over joined relations along a specific symbol.

Now given we have our factor in listing representation how do we go on and solve e.g. the Triangle Counting task? By writing the equation in the way we did, we naturally imposed a variable order in the aggregations.

We take the first variable, in this case $x_{3}$, and join all factors that contain this specific one. Joining in the sense that we multiply their respective values given their input variable instances intersect. We then apply the specified aggregation to eliminate the variable and end up with a new factor that includes the union of the variable of the two prior factors, minus the one we just aggregated. And then we continue on with the next variable in order until we are done.

In essence we reformulate our task into a dynamic programming problem and use variable elimination to solve it. This dynamic programming problem is best thought of as a hypergraph.

The induced hypergraph can be seen here.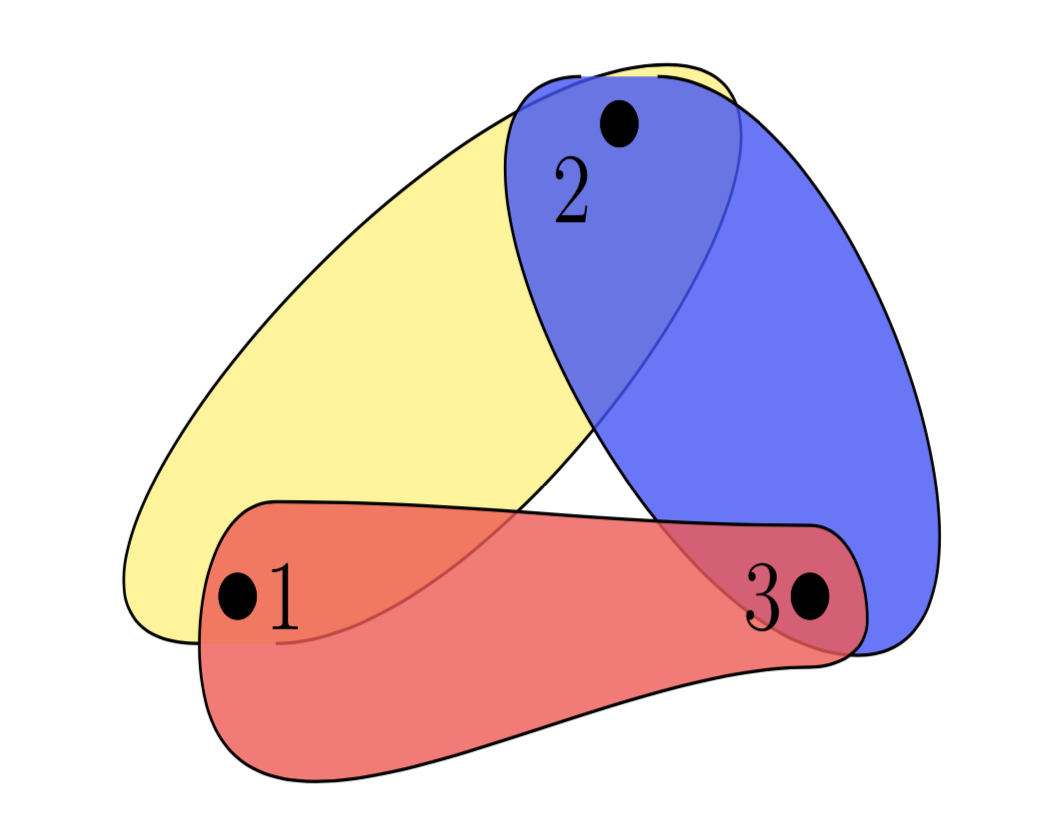

(I gave tikz a shot and only nearly cried twice).

Functional Aggregate Queries

In general the FAQ problem is to compute:

$$\varphi(\boldsymbol{\text{x}}_{[f]}) \, = \, \underset{x_{f+1} \in \text{Dom}(X_{f+1})}{\bigoplus^{(f+1)}} \quad ... \quad \underset{x_{n} \in \text{Dom}(X_{n})}{\bigoplus^{(n)}} \bigotimes_{S \in \mathcal{E}} \psi_{S}(\boldsymbol{\text{x}}_{S})$$

where:

• $\mathcal{H} = (\mathcal{V}, \mathcal{E})$ is a multi-hypergraph

• For every hypergraph edge $S\in\mathcal{E},\psi_{S} : \prod_{i \in S} \text{Dom}(X_{i}) \rightarrow \boldsymbol{D}$

• For every bound variable $i>f, \oplus^{(i)}$ is a binary aggregate operator on Domain $\boldsymbol{D}$

• For every bound variable $(\boldsymbol{D}, \oplus^{(i)}, \otimes)$ forms a commutative semiring

A semiring is made up of a Domain $\boldsymbol{D}$ and two monoids $\oplus, \otimes$, wheres the $\oplus$ distributes over the $\otimes$. A monoid consists of a binary operator and a neutral element, but no inverse. Instances of the FAQ problem induce an underlying multi-hypergraph, which represents the algebraic structure.

How do we go on and solve a FAQ?

The paper describes a general solution scheme called InsideOut, that at least for our purpose does what I intuitively explained above. We iteratively solve a given FAQ instance in the order given by starting with the most inner variable, eliminating it by applying its corresponding aggregation and moving on the next one. From the inside out.

The authors then go on and prove optimal run times given we have the best variable order.

That leaves us with a general solution to all problems that can be phrased as a FAQ.

For a more formal and thorough analysis please do read the paper. What I also am not at all concerned about, and what the authors take a big portion of time taking care of is finding the optimal variable order to guarantee worst-case optimal run time and such things.

Differential Dataflow

Okay the basics of FAQ's are set, but why should we choose differential dataflow to implement it? First a few words about the system itself: The GitHub reads:

Differential dataflow is a data-parallel programming framework designed to efficiently process large volumes of data and to quickly respond to arbitrary changes in input collections

So, in essence, it is a distributed stream processor whose operators are incrementally implemented.

If we take a look at the way we model computations in the FAQ setting we can find proper analogs in differential dataflow, that is why we started this after all!

Multiplication is done as a join, aggregation via the reduce operator and factors are modeled as differential dataflow collections.

The reason why we can take a system like differential dataflow and implement a setting like FAQ in it, is its generality and ability to directly use the type system to encode mathematical invariants and guarantees.
Let us see that in action.

The collection is differential dataflows main data structure.

This is its signature:

pub struct Collection<G: Scope, D, R: Monoid = isize> {
	pub inner: Stream<G, (D, G::Timestamp, R)>
}

A collection internally has a timely dataflow ^[4] stream that consists of elements that are triples of type D, a timestamp and a monoid R which defaults to isize.

We can best think of a Collection as a sequence of immutable tuples at distinct logical timestamps while the Diff represents their multiplicity. If we add a tuple to the collection it is +1 if we retract one it is -1.

The interesting part is that we can provide our own type there.

Lets go and build our own Diff type encoding a MaxProd semiring.

pub struct MaxProd {
        pub value: u32,
}

If we take a look at the signature of the monoid trait:

pub trait Monoid : for<'a> AddAssign<&'a Self> + ::std::marker::Sized + Data + Clone {
/* snip */
}

we see that we basically only need to implement Rusts AddAssign trait. It is only a monoid after all. To make it a semiring we need a multiplication operator. When we provide it we can use our newly defined type as a differences type for a collection.

impl<'a> AddAssign<&'a Self> for MaxProd {
        fn add_assign(&mut self, rhs: &MaxProd) {
                *self = MaxProd {
                        value: std::cmp::max(self.value, rhs.value),
                }
        }
}

impl Mul<Self> for MaxProd {
        type Output = Self;
        fn mul(self, rhs: Self) -> Self {
                MaxProd {
                        value: self.value * rhs.value,
                }
        }
}

We can implement the Monoid trait that only consists of two methods zero() and is_zero(). These tell differential dataflow when accumulations of updates equal zero (That is e.g. important to know if we are doing fix-point iteration and want to know when to stop).

impl Monoid for MaxProd {
    fn zero() -> MaxProd {
        MaxProd { value: 0 }
    }
}

And that is it. is_zero() has a default implementation.

Now, why is it interesting to encode this semiring directly as the differences type?
Because the join operator applies the Mul operation whilst joining and when we accumulate updates, e.g. with the consolidate operator or in reduce, we apply AddAssign.
The idea behind accumulation and consolidation is that we merge triples whose data part and timestamp are identical. In our case, the Data part of our collection only contains indexing variables (edges in the case of the triangle computation or matrix indices for the chain multiplication) but no actual values. In the process of eliminating a variable, we may produce a multiplicity of triples with the same indices. These are consolidated by applying the AddAssign operator, one of our monoids.

We can evaluate our FAQ simply by joining collections and consolidating the result.

Tying things together

We implement the FAQ semiring as our Diff type and move the variables to the data plane. That means every listing in the listing representation is one triple in the collection. Now insideOut is simply the repeated application of the join operator and a reduce to eliminate variables. I did a naive and simple implementation of that and a few semi rings over here:^[5] (That is partly broken right now though. I promise better)

fn inside_out(self) -> T {
        // Reduce over factors, variables and aggregates to return a faq instance over only free variables
        let faq = self
                .variable_order
                .into_iter()
                .fold(self.factors, |mut factors, var| {
                        let hyper_edges: Vec<T> = factors.drain_filter(|x| x.participate(&var)).collect();
                        let factor_prime = eliminate(join(hyper_edges), var);
                        factors.push(factor_prime);
                        factors
                });
        // Join the remaining factors to produce the output representation
        /* snip */
}

Internally eliminate and join apply the differential dataflow operators.

Currently this only works for single semiring applications of the FAQ setting.

The output coming from inside_out is simply another collection whose output is the evaluation of the FAQ.

Incrementalize it!

Now that we expressed, at least a rather naive, FAQ framework in differential dataflow, we can turn to the interesting things.

Does this incrementalize functional aggregate queries, or some instances of it?

For this, we need to do a bit of math.

Single Semiring FAQ's represent all these instances that only have a single semiring. The examples shown at the beginning are SS-FAQ instances. To show that it is possible to incrementalize a FAQ instance we need commutativity between all aggregations. This is naturally only given, without loss of generality, when there is only one semiring.

$$\begin{aligned} \overline{\varphi}(\boldsymbol{\text{x}}_{[f]}) \, &= \, \underset{x_{f+1}}{\bigoplus^{(f+1)}} \, ... \, \underset{x_{n}}{\bigoplus^{(n)}} \bigotimes_{S \in \mathcal{E}} \psi_{S}(\boldsymbol{\text{x}}_{S}) \\ &= \, \underset{x_{f+1}}{\bigoplus} \, ... \, \underset{x_{n}}{\bigoplus} \bigotimes_{S \in \mathcal{E} - S^{'}} \psi_{S}(\boldsymbol{\text{x}}_{S}) \otimes \left( \psi_{S^{'}}(\boldsymbol{\text{x}}_{S^{'}}) \bigoplus^{(n)} \delta_{\boldsymbol{\text{x}}_{S^{'}}}\right) \\ &= \, \varphi(\boldsymbol{\text{x}}_{[f]}) \bigoplus^{(n)} \delta \varphi(\boldsymbol{\text{x}}_{[f]}) \end{aligned}$$

The equation above shows that incremental properties hold. We start with a given FAQ instance. Then we assume an update occurs to factor $\psi_{S^{'}}(\boldsymbol{\text{x}}_{S^{'}})$ that regards variable $n$, namely $\delta_{\boldsymbol{\text{x}}_{S^{'}}}$. Observe that we distribute the $\bigoplus^{(n)}$ over the multiplication. Now commutativity is important as we push the remaining $n-1$ aggregations through $\bigoplus^{(n)}$. We can then compute the original part of the FAQ that leads to the left result. The right part: $\delta \varphi(\boldsymbol{\text{x}}_{[f]})$ represents the incremental update. Here we only need to compute the result with the single update $\delta_{\boldsymbol{\text{x}}_{S^{'}}}$. To get the new result to our FAQ instance, we only need to take the already computed value: $\varphi(\boldsymbol{\text{x}}_{[f]})$ and apply the aggregate to the update.

Incrementality in the sense of the above statement holds.

The beauty of implementing the FAQ setting in differential dataflow is that operators like join are already internally incrementally implemented (that is the whole point). That means by phrasing our computation with differential dataflow joins and monoidal reducees we incrementalized it.

We may start with a batch of inputs for our factors and evaluate the FAQ computation for a specific time, say $t_{0}$. Sometime later, say $t_{5}$ there are novel inputs and we incrementally update the evaluation, because internally it is just a bunch of joins. These novel inputs might even be retractions (for that our semiring needs to be an abelian group to allow for inverse elements). Updating the result just takes a fraction of the time.

Conclusion

Well, this was quite a fun project.

I think there are a few very interesting things to point out.

• The power of rusts type system to let us enforce mathematical

• invariants statically and sanely.

• The surprising generality of differential dataflow.

• How amazing differential dataflows join is.

• The power and versatility of relational algebra and the FAQ framework to express a lot of common problems.

And I haven't even started talking about running this in a distributed setting.

Next Time:

Until now we did not see the whole thing in action. That must wait for another blog post though. I'll implement a few more FAQ's in this incremental setting and we will have a look at the run times.

[1]	Frank McSherry has a GitHub repository called blog

[2]	The arxiv version of the paper

[3]	Differential Dataflow

[4]	Timely Dataflow

[5]	My partial implementation